1.2 Magnitudes Fundamentales, Derivadas, Escalares, y Vectoriales.

Magnitudes Fundamentales

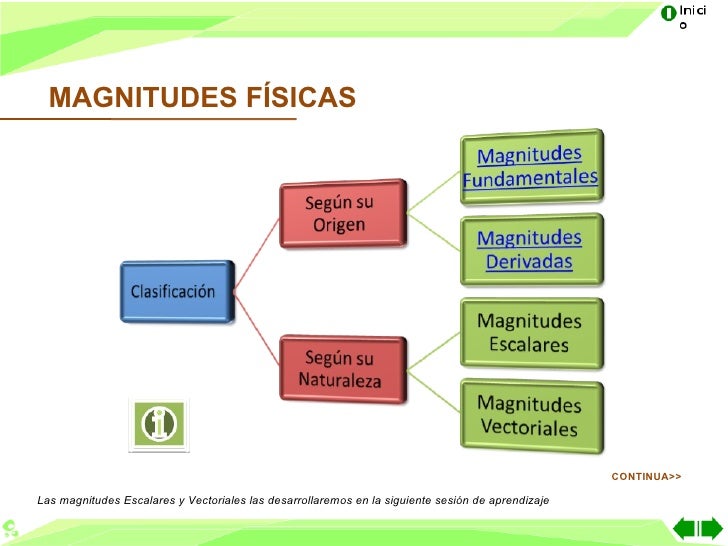
Las magnitudes fundamentales y derivadas son las magnitudes físicas que permiten expresar cualquier cantidad o medición de los cuerpos. Las magnitudes que no dependen de ninguna otra magnitud física para su medición se conocen como magnitudes fundamentales.
Estas unidades no se definen de forma independiente, ya que dependen de la definición de otras unidades. Las cantidades asociadas a las unidades derivadas se denominan magnitudes derivadas.

Magnitudes Derivadas 

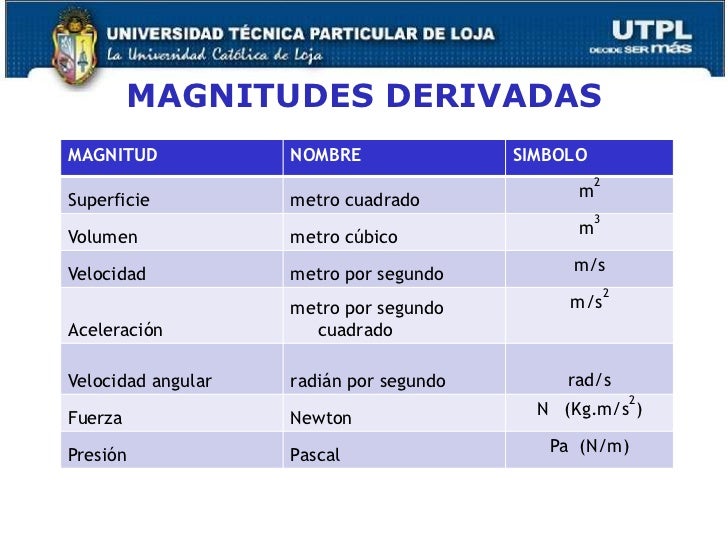
Son aquellas que derivan de las fundamentales como algunas de ellas se pueden ser definidas o indefinidas

Todas las magnitudes físicas restantes se definen como combinación de las magnitudes físicas definidas como fundamentales.
Las magnitudes derivadas están formadas por el producto de las potencias de las unidades fundamentales. En otras palabras, estas cantidades derivan del uso de las unidades fundamentales.

Magnitudes Escalares
Las magnitudes escalares tienen únicamente como variable a un número que representa una determinada cantidad. La masa de un cuerpo, que en el Sistema Internacional de Unidades se mide en kilogramos, el volumen, que se mide en metros cúbicos, la temperatura o la longitud, son algunos ejemplos de magnitudes escalares.

Magnitudes Vectoriales 

En muchos casos las magnitudes escalares no nos dan información completa sobre una propiedad física.
Por ejemplo una fuerza de determinado valor puede estar aplicada sobre un cuerpo en diferentes sentidos y direcciones. Tenemos entonces las magnitudes vectoriales que, como su nombre lo indica, se representan mediante vectores, es decir que además de un módulo (o valor absoluto) tienen una dirección y un sentido.